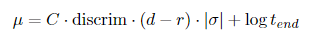解答時間推定における intercept の値について

[key-moon]

概要

解答時間推定においての intercept の値をln(contestTime)に固定してしまった方がモデルとしては正しいと思われます。

詳細

解答時間の従うモデルを以下のように導出してみました:

難易度の定義より、レート r の参加者が難易度 d の問題を終了時刻 t_{end} において正答できている確率は問題毎の定数 discrim を用いて

と表せる。
ここで、あるレート r において正答を得られるまでの時間 t は対数正規分布に依り、すべての t について対数スケールでの分散が一定であると仮定する。
そのため、あるレート r に対して対数スケールでの解答時間の中央値が e^μ、同じく分散が σ^2 のとき、時間 t に対する確率密度関数は

となる。
ここで、正規分布は定数 C≈1.7 によって尺度 s=C|σ| のロジスティック分布に近似できるため、そのような近似を用いて μ を s の式で表すことを考える。この μ,s は、時間 t に対する対数ロジスティック分布の累積分布関数 1/1+exp((μ-log t)/s) とレートあたりの正答率の式 (1) より、

という式に従う。また、これを σ に対する式とすると、

となる。

この結果は、AtCoder の問題を解くのにかかる時間をモデリングした にて「解答時間の対数の平均は1次関数に従う」と記されているものと一致します。
ここで、件の「解答時間の対数の平均」はμであることが分かります。このμの切片はln(contestTime)であるため、概要の結論を導きました。

検証

新ABC に絞ってデータを集計してみました。

	A	B	C	D	E	F
avg	6.024545997	6.687260618	7.633615235	8.391599279	8.50844374	7.958183507
med	6.017776683	6.605093961	7.701052326	8.421621444	8.649164186	8.583980336

低難易度帯については安定しませんが、高難易度帯についてはln(100*60)=8.69951475 と近い値になっているという印象を受けます。つまり、この変更を適用した際には低難易度帯の推定時間に少し変化があると予想されます。

また、長時間コンテスト（主に AGC 系列）についても検証してみたところ、予測されるような intercept の増加が見受けられました。

	time	ln(time*60)	A	B	C	D	E	F
agc049	200	9.392661928770137	9.452750561110271	9.791285737791405	9.7615837006046	10.394303855873897	0	0
agc048	150	9.104979856318357	8.83177500238767	8.979662852285616	9.610673610133812	9.180519564863609	0	0
acl1	150	9.104979856318357	9.948066763356653	9.99541723681656	10.018541028952216	9.126606093044598	9.235552693968431	0
agc047	140	9.035986984831405	9.654789237239758	9.393221736024461	9.658230533854768	9.196613999189703	8.948679930503042	0
agc046	150	9.104979856318357	7.6578514669544555	9.213359724331687	9.546185396616945	9.443326777066297	0	0
agc045	150	9.104979856318357	10.264246873449101	9.838588649482373	9.706074089017285	0	0	0
agc044	150	9.104979856318357	9.149208009507149	9.417645098345188	8.96127120865903	9.744329556275893	0	0
agc043	150	9.104979856318357	9.001965703019499	9.852419569563702	9.217822221170174	9.876969676734948	0	0

補足

モデルの導出の式が間違っていたり、置いている仮定が異なっていたりするかもしれないです。（ブログでは - 分散はレーティングによらない定数 と記されていますが、上記の導出では対数をとった正規分布の分散を定数としています）

[amylase]

難易度の定義を「コンテスト終了までに正解できる確率」と読むのはかなり筋が良さそうで感動しています。というのもこれによって解答時間と難易度のモデルを結びつけることができるからです。

特に、これと累積正規分布をロジスティック分布で近似して導出した最後の式はかなり夢を感じていて、σ をなんとかして固定するなりグリッドサーチで決めるなりすれば、discrim, d * discrim を重みとする線形モデルですから、正解時間の情報を利用して難易度が推定できそうです（今よりかなり正確になることが期待されます）。
σ は AtCoder の勝率予測式と早解き勝負の勝率予測式の整合性を取ることにすれば、 （何かしらの式）= ln(6) / 400 を使って固定できそうです。

[amylase]

難易度の定義を時間に結びつける話だと実は #808 の内容もやや関連していて（私はこういうきれいなモデルが出てくるとは思っていませんでしたが）、切片を t_end ではなく 3600 [sec] にするなどするのも意味があるかもしれません。
こう考えると、切片を固定するのは時間を正確に予測するためというよりは、難易度との整合性を図るためという感じがしますね。
（コンテスト時間の長さそのものによって解答時間モデルの切片が変化するとは考えられないので。これは本質的には問題とコンテスト参加者のみに依存するはずです）

[amylase]

色々書いてしまいましたが、私の意見を要約すると次のようになります。

• モデルの導出は、難易度の定義から派生する方式として正しそう。
• 切片がコンテスト時間で決定されるのは原理的に考えるとおかしい気がする。難易度の定義を参照したために 推定難易度がコンテスト時間に影響を受けてしまう #808 で指摘されているのと同じ欠点を引き継いだのだと考えられる
• 導出に使われている議論は時間モデルと難易度モデルの統合に使えそうで、これは研究の余地がある
• この方針を突き詰めるなら、推定難易度がコンテスト時間に影響を受けてしまう #808 を直しつつ時間モデルと難易度モデルを統合することになりそう
• 統合することで、難易度推定に時間の情報を利用できるようになり推定精度が上がりそう。（特に低難易度）

[key-moon]

ありがとうございます。難易度の定義を引き継いでしまっていて、同様の問題が起きているというのはまさにその通りだと思います。
解答時間の切片が変わるのはおかしいというのは明らかにそうですね。上の式では

μ = C·discrim·(d−r)·|σ|+ log(t_{end})

としていましたが、定義の式と取っている切片の位置が異なっていました……（申し訳ない）
式 slope * r + intercept に当てはめる場合は

μ = -C·discrim·|σ|·r+(C·discrim·|σ|·d+log(t_{end}))

として

slope = -C·discrim·|σ|
intercept = C·discrim·|σ|·d+log(t_{end})=log(t_{end})-slope·d

となるというのが正しそうですね。d にての切片が log(t_end) で、d-d での切片が log(t_end)-slope·d という解釈も、直感的に納得ができます。そこまで意味のある分析にはならないと思われますが、これに基づいて現状の slope から切片を求めたものとの差を求めてみました。(現状 - log(t_end)-slope*d )

値が問題難易度によらず一定の位置にまとまっているので、良い性質がありそうに見えます。
これについては、現状の線形回帰分析では、コンテスト終了後に正答するはずであったデータがないために「早く解けた方に引っ張られて」しまっているのではないかと考えます。

[key-moon]

解答時間の情報を利用した難易度推定についてですが、この式自体がコンテスト中の最終難易度推定を研究している時に出てきた式なので少しだけ知見を提供できる気がします。これは別 issue を建てたほうが良さそうな気がするので、現状の進展を別途書かせて頂きます。

[amylase]

あたらしく上げていただいたグラフなんですが、私には難易度（というかスロット（ABCDEFの位置））に依存して切片が変化しているように見えます。

現状の線形回帰分析では、コンテスト終了後に正答するはずであったデータがないために「早く解けた方に引っ張られて」しまっているのではないかと考えます。

これについては過去に少し是正を試みたことがあって ( #290 )、要約すると正答するはずのデータが観測できない欠損値を潜在変数として同時に推定してみたんですが、当時はあんまりうまく行きませんでした。
後ろの問題のほうが欠損の影響を受けやすい（そもそも時間がかかる＋前の問題で時間を取られる）ので、前の問題がより早く解けた方に引っ張られがちだと思うと私のグラフの解釈とも一致しますが、いかがでしょうか？
とすると後ろの問題のほうがより引っ張られているはずなんですが、謎いですね（まずグラフの解釈が難しいですが）。

[amylase]

欠損（統計的に厳密には打ち切りと呼ぶほうが正しいらしいです）は、コンテスト中のデータから最終難易度を推定するなら避けては通れない問題だと思うので、なんとかいい方法があるといいんですけどね……